长为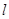 的不计形变的轻绳,一端固定在O点,另一端系一质量为
的不计形变的轻绳,一端固定在O点,另一端系一质量为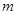 小球,在O下方
小球,在O下方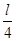 处,将小球水平向右抛出,忽略空气阻力的影响,经过一段时间绳拉直(绳刚拉直时与竖直线夹角
处,将小球水平向右抛出,忽略空气阻力的影响,经过一段时间绳拉直(绳刚拉直时与竖直线夹角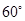 );最后又摆动经过最低点。
);最后又摆动经过最低点。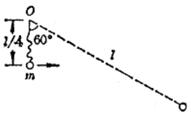
求:
(1)球水平抛出的速度;
(2)球摆到最低点时,绳所受拉力。
长为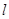 的不计形变的轻绳,一端固定在O点,另一端系一质量为
的不计形变的轻绳,一端固定在O点,另一端系一质量为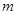 小球,在O下方
小球,在O下方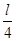 处,将小球水平向右抛出,忽略空气阻力的影响,经过一段时间绳拉直(绳刚拉直时与竖直线夹角
处,将小球水平向右抛出,忽略空气阻力的影响,经过一段时间绳拉直(绳刚拉直时与竖直线夹角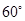 );最后又摆动经过最低点。
);最后又摆动经过最低点。
求:
(1)球水平抛出的速度;
(2)球摆到最低点时,绳所受拉力。