如图所示,MN表示真空室中垂直于纸面放置的感光板,它的一侧有方向垂直于纸面向里匀强磁场. 一个质量为m,电荷量为q的带电粒子从感光板上的狭缝O处以垂直于感光板的初速度v射入磁场区域,最后到达感光板上的P点. 经测量P、O间的距离为L,不计带电粒子受到的重力. 求:
(1)该粒子带正电还是负电?
(2)带电粒子由O运动到P所用的时间t;
(3)匀强磁场的磁感应强度B.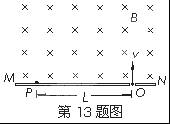
相关知识点
如图所示,MN表示真空室中垂直于纸面放置的感光板,它的一侧有方向垂直于纸面向里匀强磁场. 一个质量为m,电荷量为q的带电粒子从感光板上的狭缝O处以垂直于感光板的初速度v射入磁场区域,最后到达感光板上的P点. 经测量P、O间的距离为L,不计带电粒子受到的重力. 求:
(1)该粒子带正电还是负电?
(2)带电粒子由O运动到P所用的时间t;
(3)匀强磁场的磁感应强度B.