如图所示，一质量为M的平板车B放在光滑水平面上，在其左端放一质量为m的小木块A，m<M，A、B间动摩擦因数为μ，现同时给A和B大小相等、方向相反的初速度v0，使A开始向右运动，B开始向左运动，最后A不会滑离B。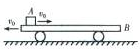
求：
①A、B最后的速度大小和方向；
②A在B上相对滑动的时间，
分如图甲所示，MN、PQ为间距L=0．5m足够长的平行导轨，NQ⊥MN，导轨的电阳均不计。导轨平面与水平面间的夹角
=37°，NQ间连接有一个R=4
的电阻。有一匀强磁场垂直于导轨平面且方向向上，磁感应强度为B0=1T。将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上，且与导轨接触良好。现由静止释放金属棒，当金属棒滑行至cd处时达到稳定速度，已知在此过程中通过金属棒截面的电量q=0.2C，且金属棒的加速度a与速度v的关系如图乙所示，设金属棒沿导轨向下运动过程中始终与NQ平行。取g=10m／s2。求：
（1）金属棒与导轨间的动摩擦因数μ；
（2）cd离NQ的距离s；
（3）金属棒滑行至cd处的过程中，电阻R上产生的热量；
（4）若将金属棒滑行至cd处的时刻记作t=0，从此时刻起，让磁感应强度逐渐减小，为使金属棒中不产生感应电流，则磁感应强度B应怎样随时间t变化?
分如图所示，某放射源A中均匀地向外辐射出平行于y轴的、速度一定的a粒子(质量为m，电荷量为+q)。为测定其飞出的速度大小，现让其先经过一个磁感应强度为B、区域为半圆形的匀强磁场，经该磁场偏转后，它恰好能够沿x轴进入右侧的平行板电容器，并打到置于N板上的荧光屏上。调节滑动触头，当触头P位于滑动变阻器的中央位置时，通过显微镜头Q看到屏上的亮点恰好能消失．已知电源电动势为E，内阻为r0，滑动变阻器的总阻值R0="2" r0，问：
(1)a粒子的速度大小v0=?
(2)满足题意的a粒子，在磁场中运动的总时间t=?
(3)该半圆形磁场区域的半径R=?
分如图(a)所示，一质量为m的滑块(可视为质点)沿某斜面顶端A由静止滑下，己知滑块与斜面间的动摩擦因数μ和滑块到斜面顶端的距离x的关系如图(b)所示。斜面倾角为37。，长为l，求：
(1)滑块滑至斜面中点时的加速度大小；
(2)滑块滑至斜面底端时的速度大小。
(15分)如图所示，为一磁约束装置的原理图，圆心为原点O、半径为R0的圆形区域Ⅰ内有方向垂直xoy平面向里的匀强磁场。一束质量为m、电量为q、动能为E0的带正电粒子从坐标为(0、R0)的A点沿y轴负方向射入磁场区域Ⅰ，粒子全部经过x轴上的P点，方向沿x轴正方向。当在环形区域Ⅱ加上方向垂直于xoy平面的匀强磁场时，上述粒子仍从A点沿y轴负方向射入区域Ⅰ，粒子经过区域Ⅱ后从Q点第2次射入区域Ⅰ，已知OQ与x轴正方向成600。不计重力和粒子间的相互作用。求：
(1)区域Ⅰ中磁感应强度B1的大小；
(2)若要使所有的粒子均约束在区域内，则环形区域Ⅱ中B2的大小、方向及环形半径R至少为大；
(3)粒子从A点沿y轴负方向射入后至再次以相同的速度经过A点的运动周期。
的液珠仍从A 处静止释放时，问能否运动到原来的最大高度B点？若能，则此时经过B点的速度为多大？
粤公网安备 44130202000953号