(12分)在如图所示的直角坐标系xoy中,矩形区域oabc内有垂直于纸面向外的匀强磁场,磁感应强度大小为B=5.0×10-2T;第一象限内有沿-y方向的匀强电场,电场强度大小为E=1.0×105N/C.已知矩形区域oa边长为0.60m,ab边长为0.20 m.在bc边中点N处有一放射源,某时刻,放射源沿纸面向磁场中各方向均匀地辐射出速率均为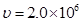 m/s的某种带正电粒子,带电粒子质量m=1.6×10-27kg,电荷量为q=+3.2×10-19kg,不计粒子重力,求:(计算结果保留两位有效数字)
m/s的某种带正电粒子,带电粒子质量m=1.6×10-27kg,电荷量为q=+3.2×10-19kg,不计粒子重力,求:(计算结果保留两位有效数字)
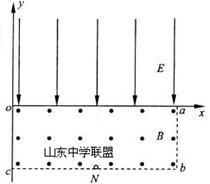
(1)粒子在磁场中运动的半径;
(2)从x轴上射出的粒子中,在磁场中运动的最短路程为多少?
(3)放射源沿-x方向射出的粒子,从射出到从y轴离开所用的时间.