如图所示,一带电粒子以与水平方向成60°角速度在竖直平面内做直线运动,经过一段时间后进入一垂直于纸面向里、磁感应强度为B的圆形匀强磁场区域(图中未画出磁场区域),粒子飞出磁场后垂直电场方向进入宽为L的匀强电场。 电场强度大小为E,方向竖直向上。当粒子穿出电场时速度大小变为原来的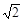 倍。 已知带电粒子的质量为m,电量为q,重力不计。求:
倍。 已知带电粒子的质量为m,电量为q,重力不计。求: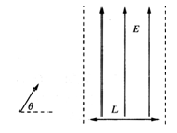
(1)粒子带什么电?简述理由;
(2)带电粒子在磁场中运动时速度多大;
(3)该圆形磁场区域的最小面积为多大。
如图所示,一带电粒子以与水平方向成60°角速度在竖直平面内做直线运动,经过一段时间后进入一垂直于纸面向里、磁感应强度为B的圆形匀强磁场区域(图中未画出磁场区域),粒子飞出磁场后垂直电场方向进入宽为L的匀强电场。 电场强度大小为E,方向竖直向上。当粒子穿出电场时速度大小变为原来的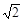 倍。 已知带电粒子的质量为m,电量为q,重力不计。求:
倍。 已知带电粒子的质量为m,电量为q,重力不计。求:
(1)粒子带什么电?简述理由;
(2)带电粒子在磁场中运动时速度多大;
(3)该圆形磁场区域的最小面积为多大。