如图所示，在长为2L、宽为L的区域内正好一半空间有场强为E、方向平行于短边的匀强电场，有一个质量为ｍ，电量为ｅ的电子，以平行于长边的速度v0从区域的左上角A点射入该区域，不计电子所受重力，要使这个电子能从区域的右下角的B点射出，求：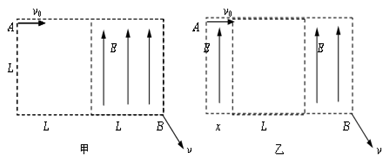
（1）无电场区域位于区域左侧一半内时，如图甲所示，电子的初速度应满足什么条件；
（2）无电场区域的左边界离区域左边的距离为x时，如图乙所示，电子的初速度又应满足什么条件。
如图所示，质量为2.0kg的木块放在水平桌面上的A点，受到一冲量后以某一速度在桌面上沿直线向右运动，运动到桌边B点后水平滑出落在水平地面C点。已知木块与桌面间的动摩擦因数为0.20，桌面距离水平地面的高度为1.25m，A、B两点的距离为4.0m，B、C两点间的水平距离为1.5m，g=10m/s2。不计空气阻力，求：
（1）桌面对木块滑动摩擦力做功的大小；
（2）木块在A点时的动能；
（3）木块运动的总时间。
如图所示，质量m=2.0kg的金属块放在水平地板上，在与水平方向成θ=37°角斜向上、大小为F=10N的拉力作用下，以速度v=5.0m/s向右做匀速直线运动。
（cos37°=0.8，sin37°=0.6，取g=10m/s2）求：
（1）撤去拉力后物体运动的加速度；
（2）撤去拉力后物体运动的最长时间。
(10分)如图所示，质量m＝0.1g的小物块，带有5×10-4C的电荷，放在倾角为30°的光滑绝缘斜面上，整个斜面置于B=0.5T的匀强磁场中，磁场方向垂直纸面指向纸里，物块由静止开始下滑，滑到某一位置时，开始离开斜面，求：
（1）物块带什么电？
（2）物块离开斜面时速度多大？
（3）斜面至少有多长？
(10分) 如图所示，半径为 r、电阻不计的两个半圆形光滑导轨并列竖直放置，导轨端口所在平面刚好水平。在轨道左上方端口M、N 间接有阻值为R 的小电珠，整个轨道处在磁感应强度为B 的匀强磁场中，两导轨间距为L，现有一质量为 m，电阻也是R 的金属棒ab 从MN 处由静止释放，经一定时间到达导轨最低点 OO¢ ，此时速度为 v 。
（1）求金属棒 ab 到达 OO¢ 时，受到的安培力的大小和方向。
（2）求金属棒 ab 从MN 到 OO¢ 的过程中，小电珠上产生的热量。
粤公网安备 44130202000953号