如图所示，在水平地面上有一向右匀速行驶的车，车内用绳AB与绳BC拴住一个小球，BC绳水平，AB绳与竖直方向夹角θ为37°，小球质量为0.8 kg，小球在车中位置始终未变(g取10 m/s2，sin 37°＝0.6，cos 37°＝0.8)．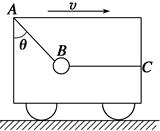
求：(1)小球对AB绳的拉力大小；
(2)小球对BC绳的拉力大小．
如图甲所示，光滑且足够长的平行金属导轨MN、PQ固定在同一水平面上，两导轨间距L=0.30m。导轨电阻忽略不计，其间接有固定电阻R=0.40Ω.导轨上停放一质量为m=0.10kg、电阻r=0.20Ω的金属杆ab，整个装置处于磁感应强度B=0.50T的匀强磁场中，磁场方向竖直向下。利用一外力F沿水平方向拉金属杆ab，使之由静止开始做匀加速直线运动，电压传感器可将R两端的电压U即时采集并输入电脑，并获得U随时间t的关系如图乙所示。求：
（1）金属杆加速度的大小；
（2）第2s末外力的瞬时功率。
(14分)如图，在倾角θ=53°的固定斜面上放置一质量M=1kg、长度l=3m的薄平板AB。平板的上表面光滑，其下端B与斜面底端C的距离为L=9m。在平板的上端A处放一质量m=1kg的小滑块，开始时使平板和滑块都静止，之后将它们无初速释放。设平板与斜面间、滑块与斜面间的动摩擦因数均为μ=0.5，不考虑滑块由平板落到斜面的速度变化。求：(sin53°=0.8，cos53°=0.6，g=10m/s2)
(1)滑块离开平板时的速度大小；
(2)滑块从离开平板到到达斜面底端C经历的时间；
(3)滑块到达C处时，平板的B端与C的距离。
(12分)如图所示，在无限长的竖直边界AC和DE间，上、下部分分别充满方向垂直于ADEC平面向外的匀强磁场，上部分区域的磁感应强度大小为B0，OF为上、下磁场的水平分界线。质量为m、带电荷量为+q的粒子从AC边界上与O点相距为a的P点垂直于A C边界射入上方区域，经OF上的Q点第一次进入下方区域，Q与O点的距离为3a。不考虑粒子重力
(1)求粒子射入时的速度大小；
(2)要使粒子不从AC边界飞出，求下方区域的磁感应强度应满足的条件；
(3)若下方区域的磁感应强度B=3B0，粒子最终垂直DE边界飞出，求边界DE与AC 间距离的可能值。
(10分)如图所示，倾角θ=30°、宽L=1m的足够长的U形光滑金属导轨固定在磁感应强度大小B=IT、范围足够大的匀强磁场中，磁场方向垂直导轨平面向上。一根质量m=0.2kg，电阻R=l
的金属棒ab垂直于导轨放置。现用一平行于导轨向上的牵引力F作用在棒上，使棒由静止开始沿导轨向上运动，运动中ab棒始终与导轨接触良好，导轨电阻不计，重力加速度g取l0m/s2。求：
(1)若牵引力的功率P恒为56W，则ab棒运动的最终速度为多大?
(2)当ab棒沿导轨向上运动到某一速度时撤去牵引力，从撤去牵引力到ab棒的速度为零，通过ab棒的电量q=0.5C，则撤去牵引力后ab棒向上滑动的距离多大?
滑下，到C点后压缩弹簧进入水平轨道，被弹簧反弹后恰能通过B点。重力加速度为g，求：
粤公网安备 44130202000953号