如图所示,绷紧的传送带,始终以v=2m/s的速度匀速斜向上运行,传送带与水平方向间的夹角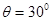 .现把质量m=10kg的工件轻轻地放在传送带底端P处,由传送带传送至顶端Q处.已知PQ之间的距离为4m,工件与传送带间的动摩擦因数为
.现把质量m=10kg的工件轻轻地放在传送带底端P处,由传送带传送至顶端Q处.已知PQ之间的距离为4m,工件与传送带间的动摩擦因数为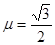 ,取g=10m/s2.
,取g=10m/s2.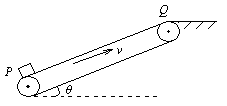
(1)通过计算说明工件在传送带上做什么运动;
(2)求工件从P点运动到Q点所用的时间.
如图所示,绷紧的传送带,始终以v=2m/s的速度匀速斜向上运行,传送带与水平方向间的夹角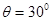 .现把质量m=10kg的工件轻轻地放在传送带底端P处,由传送带传送至顶端Q处.已知PQ之间的距离为4m,工件与传送带间的动摩擦因数为
.现把质量m=10kg的工件轻轻地放在传送带底端P处,由传送带传送至顶端Q处.已知PQ之间的距离为4m,工件与传送带间的动摩擦因数为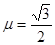 ,取g=10m/s2.
,取g=10m/s2.
(1)通过计算说明工件在传送带上做什么运动;
(2)求工件从P点运动到Q点所用的时间.