一倾角为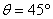 的斜面固定于地面,斜面顶端离地面的高度h0=1m,斜面底端有一垂直于斜面的固定挡板。在斜面顶端自由释放一质量m=0.09kg的小物块(视为质点)。小物块与斜面之间的动摩擦因数u=0.2。当小物块与挡板碰撞后,将以原速返回。重力加速度g="10" m/s2。在小物块与挡板的前4次碰撞过程中,挡板给予小物块的总冲量是多少?
的斜面固定于地面,斜面顶端离地面的高度h0=1m,斜面底端有一垂直于斜面的固定挡板。在斜面顶端自由释放一质量m=0.09kg的小物块(视为质点)。小物块与斜面之间的动摩擦因数u=0.2。当小物块与挡板碰撞后,将以原速返回。重力加速度g="10" m/s2。在小物块与挡板的前4次碰撞过程中,挡板给予小物块的总冲量是多少?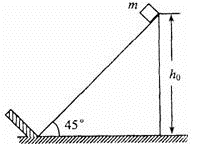
一倾角为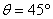 的斜面固定于地面,斜面顶端离地面的高度h0=1m,斜面底端有一垂直于斜面的固定挡板。在斜面顶端自由释放一质量m=0.09kg的小物块(视为质点)。小物块与斜面之间的动摩擦因数u=0.2。当小物块与挡板碰撞后,将以原速返回。重力加速度g="10" m/s2。在小物块与挡板的前4次碰撞过程中,挡板给予小物块的总冲量是多少?
的斜面固定于地面,斜面顶端离地面的高度h0=1m,斜面底端有一垂直于斜面的固定挡板。在斜面顶端自由释放一质量m=0.09kg的小物块(视为质点)。小物块与斜面之间的动摩擦因数u=0.2。当小物块与挡板碰撞后,将以原速返回。重力加速度g="10" m/s2。在小物块与挡板的前4次碰撞过程中,挡板给予小物块的总冲量是多少?