如图所示，长l＝0.8 m的细线上端固定在O点，下端连结一个质量为m＝0.4 kg的小球，悬点O距地面的高度H＝3.55 m，开始时将小球提到O点而静止，然后让它自由下落，当小球到达使细线被拉直的位置时，刚好把细线拉断，再经过t＝0.5 s落到地面，如果不考虑细线的形变，g＝10 m/s2，试求：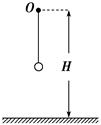
(1)细线拉断前后的速度大小和方向；
(2)假设细线由拉直到断裂所经历的时间为0.1 s，试确定细线的平均张力大小．
如图所示 ，C是静止放在光滑的水平面上的一块木板，木板的质量为2m。小木块B以2v0的初速度水平向右从木板左端滑上木板。当B与C相对静后，小木块A以v0的初速度水平向右从木板左端滑上木板。小木块A和B质量均为m，它们与木板间的动摩擦因数均为μ，且木板足够长，重力加速度为g。求：
(1)小木块B的最终速度；
(2)小木块A与小木块B最终距离。
如图甲所示，在一个正方形金属线圈区域内存在着磁感应强度B随时间变化的匀强磁场，磁场的方向与线圈平面垂直．金属线圈所围的面积S＝200 cm2，匝数n＝1 000，线圈电阻r＝1.0 Ω.线圈与电阻R构成闭合回路，电阻的
阻值R ＝4.0 Ω.匀强磁场的磁感应强度随时间变化的情况如
图乙所示，求：
(1) 在t＝2.0 s时通过电阻R的感应电流的大小；
(2) 在t＝5.0 s时刻，线圈端点a、b间的电压；
质量为2 kg的平板车B上表面水平,原来静止在光滑水平面上,平板车一端静止着一块质量为2 kg的物体A,一颗质量为0.01 kg的子弹以600 m/s的速度水平瞬间射穿A后,速度变为100 m/s。 
(1)A的最大速度;
(2)若A不会滑离B,B的最大速度是多少?
一理想降压变压器，原线圈上所加电压为11 kV，副线圈通过输电导线向用户供电，输电导线的总电阻R＝0.05 Ω，用户的用电器(假设是纯电阻)得到的电压为220 V、消耗的电功率为44 kW.求变压器原、副线圈的匝数比n1∶n2.
如图所示，装置BO′O可绕竖直轴O′O转动，可视为质点的小球A与两细线连接后分别系于B、C两点，装置静止时细线AB水平，细线AC与竖直方向的夹角θ=37º．已知小球的质量m=1kg，细线AC长l=1m， B点距C点的水平和竖直距离相等．（重力加速度g取10m/s2，
，
）（结果可以用根号表示）
（1）若装置匀速转动的角速度为ω1时，细线AB上的张力为零而细线AC与竖直方向夹角仍为37º，求角速度ω1的大小；
（2）若装置匀速转动的角速度
，求细线AC与竖直方向的夹角的余弦值；
（3）装置可以以不同的角速度匀速转动，试通过计算在坐标图中画出细线AC上张力T随角速度的平方ω2 变化的关系图象。
粤公网安备 44130202000953号