一个弹簧秤放在水平地面上,Q为与轻弹簧上端连在一起的秤盘,P为重物,已知P的质量M ="10.5" kg,Q的质量 m ="1.5" kg,弹簧的质量不计,劲度系数 k ="800" N/m,系统处于静止.如图所示,现给P施加一个方向竖直向上的力F,使它从静止开始向上做匀加速运动,已知在前0.2 s内,F为变力,0.2 s 以后,F为恒力.求力F的最大值与最小值.(取g ="10" m/s2)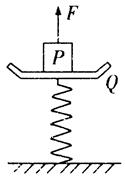
一个弹簧秤放在水平地面上,Q为与轻弹簧上端连在一起的秤盘,P为重物,已知P的质量M ="10.5" kg,Q的质量 m ="1.5" kg,弹簧的质量不计,劲度系数 k ="800" N/m,系统处于静止.如图所示,现给P施加一个方向竖直向上的力F,使它从静止开始向上做匀加速运动,已知在前0.2 s内,F为变力,0.2 s 以后,F为恒力.求力F的最大值与最小值.(取g ="10" m/s2)