如图所示,小球a被一根长为L=0.5m的可绕O轴自由转动的轻质细杆固定在其端点,同时又通过绳跨过光滑定滑轮与另一个质量为m小球b相连,整个装置平衡时杆和绳与竖直方向的夹角均为30°．若将小球a拉水平位置（杆呈水平状态）开始释放,不计摩擦,竖直绳足够长,求: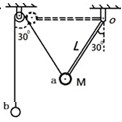
(1)小球a的质量;
(2)当杆转动到竖直位置时,小球b的速度大小．(结果可用根式表示)
如图所示，电荷量均为＋q、质量分别为m和2m的小球A和B，中间连接质量不计的细绳，在竖直方向的匀强电场中以速度v0匀速上升，某时刻细绳突然断开．求：
(1)电场强度大小及细绳断开后两球A、B的加速度；
(2)当球B速度为零时，球A的速度大小。
一半径为R的1/4球体放置在水平面上，球体由折射率为
的透明材料制成。现有一束位于过球心O的竖直平面内的光线，平行于桌面射到球体表面上，折射入球体后再从竖直表面射出，如图所示。已知入射光线与桌面的距离为
。求出射角
。
一气象探测气球，在充有压强为1.00atm（即76.0cmHg）、温度为27.0℃的氦气时，体积为3.50m3。在上升至海拔6.50km高空的过程中，气球内氦气压强逐渐减小到此高度上的大气压36.0cmHg，气球内部因启动一持续加热过程而维持其温度不变。此后停止加热，保持高度不变。已知在这一海拔高度气温为-48.0℃。求：
①氦气在停止加热前的体积；
②氦气在停止加热较长一段时间后的体积。
如右图所示，在一个圆形区域内，两个方向相反且都垂直于纸面的匀强磁场分布在以直径A2A4为边界的两个半圆形区域Ⅰ、Ⅱ中，A2A4与A1A3的夹角为60°。一质量为m，带电量为+q的粒子以某一速度从Ⅰ区的边缘点A1处沿与A1A3成30°角的方向射入磁场，随后该粒子以垂直于A2A4的方向经过圆心O进入Ⅱ区，最后再从A4处射出磁场。已知该粒子从射入到射出磁场所用的时间为t,求Ⅰ区和Ⅱ区中的磁感应强度的大小。（忽略粒子重力）。
(不计空气阻力)。
粤公网安备 44130202000953号