如图甲所示,电荷量为q =1×10-4C的带正电的小物块置于绝缘水平面上,所在空间存在方向沿水平向右的电场,电场强度E的大小与时间的关系如图乙所示,物块运动速度与时间t的关系如图丙所示,取重力加速度g=10m/s2。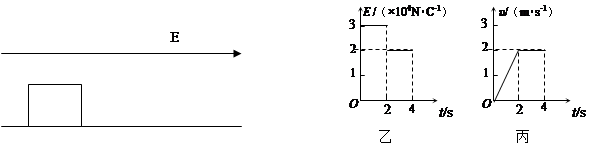
求(1)前2秒内电场力做的功。
(2)物块的质量.
(3)物块与水平面间的动摩擦因数。
如图甲所示,电荷量为q =1×10-4C的带正电的小物块置于绝缘水平面上,所在空间存在方向沿水平向右的电场,电场强度E的大小与时间的关系如图乙所示,物块运动速度与时间t的关系如图丙所示,取重力加速度g=10m/s2。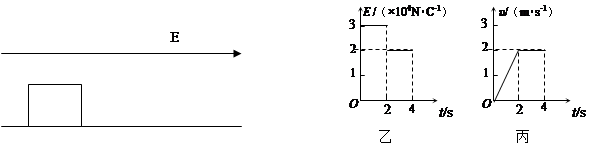
求(1)前2秒内电场力做的功。
(2)物块的质量.
(3)物块与水平面间的动摩擦因数。