如图,让一小物体(可看作质点)从图示斜面上的A点以v0=4m/s的初速度滑上斜面,物体滑到斜面上的B点后沿原路返回。若A到B的距离为1m,斜面倾角为θ=37°。(sin37°=0.6,cos37°=0.8,g=10m/s2)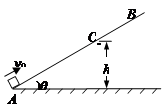
(1)求物体与斜面间的动摩擦因数;
(2)若设水平地面为零重力势能面,且物体返回经过C点时,其动能恰与重力势能相等,求C点相对水平地面的高度h。
如图,让一小物体(可看作质点)从图示斜面上的A点以v0=4m/s的初速度滑上斜面,物体滑到斜面上的B点后沿原路返回。若A到B的距离为1m,斜面倾角为θ=37°。(sin37°=0.6,cos37°=0.8,g=10m/s2)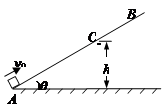
(1)求物体与斜面间的动摩擦因数;
(2)若设水平地面为零重力势能面,且物体返回经过C点时,其动能恰与重力势能相等,求C点相对水平地面的高度h。