如图所示,一轻绳通过无摩擦的定滑轮与放在倾角为30°的光滑斜上的物体m1连接,另一端和套在光滑竖直杆上的物体m2连接,图中定滑轮到竖直杆的距离为 m,又知当物体m2由图中位置(连接m2的轻绳此时水平)从静止开始下滑1m时,m1和m2受力恰好平衡。试求:(g取10 m/s2 )
m,又知当物体m2由图中位置(连接m2的轻绳此时水平)从静止开始下滑1m时,m1和m2受力恰好平衡。试求:(g取10 m/s2 )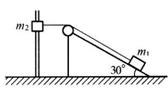
(1)m2下滑过程中的最大速度。
(2)m2下滑的最大距离。
如图所示,一轻绳通过无摩擦的定滑轮与放在倾角为30°的光滑斜上的物体m1连接,另一端和套在光滑竖直杆上的物体m2连接,图中定滑轮到竖直杆的距离为 m,又知当物体m2由图中位置(连接m2的轻绳此时水平)从静止开始下滑1m时,m1和m2受力恰好平衡。试求:(g取10 m/s2 )
m,又知当物体m2由图中位置(连接m2的轻绳此时水平)从静止开始下滑1m时,m1和m2受力恰好平衡。试求:(g取10 m/s2 )
(1)m2下滑过程中的最大速度。
(2)m2下滑的最大距离。