一个电子以v0=4×107m/s的速度,方向与电场方向相同,射入电场强度E=2×105V/m的匀强电场中,如图所示,已知电子电量-e=-1.6×10-19C,电子质量m=9.1×10-31kg.。试求:
(1)从电子的入射点到达速度为0之点的两点间电势差是多少? 两点间距离是多少?
(2)电子速度减小为0所需的时间是多少? 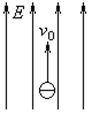
一个电子以v0=4×107m/s的速度,方向与电场方向相同,射入电场强度E=2×105V/m的匀强电场中,如图所示,已知电子电量-e=-1.6×10-19C,电子质量m=9.1×10-31kg.。试求:
(1)从电子的入射点到达速度为0之点的两点间电势差是多少? 两点间距离是多少?
(2)电子速度减小为0所需的时间是多少? 