如图所示,大量质量为m、电荷量为+q的粒子,从静止开始经极板A、B间加速后,沿中心线方向陆续进入平行极板C、D间的偏转电场,飞出偏转电场后进入右侧的有界匀强磁场,最后从磁场左边界飞出.已知A、B间电压为U0;极板C、D长为L,间距为d;磁场的磁感应强度大小为B,方向垂直纸面向里,磁场的左边界与C、D右端相距L,且与中心线垂直.假设所有粒子都能飞出偏转电场,并进入右侧匀强磁场,不计粒子的重力及相互间的作用.则:
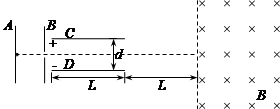
(1)求粒子在偏转电场中运动的时间t;
(2)求能使所有粒子均能进入匀强磁场区域的偏转电压的最大值U;
(3)接第(2)问,当偏转电压为U/2时,求粒子进出磁场位置之间的距离.