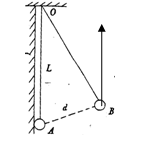
如图光滑的定滑轮上绕有轻质柔软细线,线的一端系一质量为3m的重物,另一端系一质量为m、电阻为r的金属杆.在竖直平面内有间距为L的足够长的平行金属导轨PQ、EF,在QF之间连接有阻值为R的电阻,其余电阻不计,磁感应强度为B0的匀强磁场与导轨平面垂直,开始时金属杆置于导轨下端QF处,将重物由静止释放,当重物下降h时恰好达到稳定速度而匀速下降.运动过程中金属杆始终与导轨垂直且接触良好,(忽略所有摩擦,重力加速度为g),求:

(1)电阻R中的感应电流方向;
(2)重物匀速下降的速度v;
(3)重物从释放到下降h的过程中,电阻R中产生的焦耳热QR;
(4)若将重物下降h时的时刻记作t=0,速度记为v0,从此时刻起,磁感应强度逐渐减小,若此后金属杆中恰好不产生感应电流,则磁感应强度B怎样随时间t变化(写出B与t的关系式).