(14分)如下图，竖直平面坐标系
的第一象限，有垂直面向外的水平匀强磁场和竖直向上的匀强电场，大小分别为B和E；第四象限有垂直面向里的水平匀强电场,大小也为
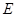；第三象限内有一绝缘光滑竖直放置的半径为
的半圆轨道,轨道最高点与坐标原点
相切,最低点与绝缘光滑水平面相切于
.一质量为
的带电小球从
轴上(
)的
点沿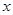
轴正方向进入第一象限后做圆周运动,恰好通过坐标原点,且水平切入半圆轨道并沿轨道内侧运动,过点水平进入第四象限,并在电场中运动(已知重力加速度为
).
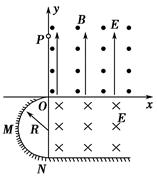
(1)判断小球的带电性质并求出其所带电荷量；
(2)点距坐标原点至少多高；
(3)若该小球以满足(2)中
最小值的位置和对应速度进入第一象限,通过点开始计时,经时间
小球距坐标原点的距离
为多远？
相关试题
如图所示，A、B是两块质量均为m的木块，它们之间的滑动摩擦因数为μ，B与地面间的滑动摩擦因数也为μ，现对A施加一个水平向右的拉力F，可使A向右，B向左都做匀速直线运动.若滑轮处的摩擦不计，则F的大小等于多少？
如图所示，一平直的传送带以速度v=2m/s匀速运动，传送带把A处的工件运送到B处，A、B相距L=10m．从A处把工件无初速地放到传送带上，经过时间t=6s能传送到B处．求：
（1）工件在传送带上做匀加速运动的时间；
（2）工件做匀加速运动的加速度大小．
在光滑水平地面上有两个相同的弹性小球A、B，质量都为m.现B球静止，A球向B球运动，发生正碰．已知碰撞过程中总机械能守恒，两球压缩最紧时的弹性势能为Ep，求：碰前A球的速度大小等于多少？
一物体在冰面上做匀减速直线运动直到停止，已知最初3s和最后3s内所通过的位移分别为16.5m和4.5m，求：（1）物体在冰面上滑行的加速度的大小，
（2）物体在冰面上滑行的总时间和总路程。
粤公网安备 44130202000953号