中子星是恒星演化过程中的一种可能结果,它的密度很大.现有一中子星,观测到
它的自转周期为T=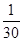 s.问该中子星的最小密度应是多少才能维持该星体的稳定,不
s.问该中子星的最小密度应是多少才能维持该星体的稳定,不
致因自转而瓦解?(计算时星体可视为均匀球体,万有引力常量G=6.67×10-11m3/(kg·s2))
中子星是恒星演化过程中的一种可能结果,它的密度很大.现有一中子星,观测到
它的自转周期为T=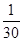 s.问该中子星的最小密度应是多少才能维持该星体的稳定,不
s.问该中子星的最小密度应是多少才能维持该星体的稳定,不
致因自转而瓦解?(计算时星体可视为均匀球体,万有引力常量G=6.67×10-11m3/(kg·s2))