如图所示,内壁光滑半径为R的圆形轨道,固定在竖直平面内.质量为m1的小球静止在轨道最低点,另一质量为m2的小球(两小球均可视为质点)从内壁上与圆心O等高的位置由静止释放,运动到最低点时与m1发生碰撞并粘在一起.求: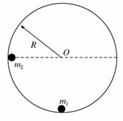
(1)小球m2刚要与m1发生碰撞时的速度大小;
(2)碰撞后,m1､m2能沿内壁运动所能达到的最大高度(相对碰撞点).
如图所示，光滑水平面上固定一半径为
的光滑水平圆形轨道，过圆心
相垂直的两虚线交圆弧于A、B、C、D四点，质量为
的乙球静置于B处，质量为
的甲球从A处沿圆弧切线方向以速度
开始运动，到达B处与乙球发生碰撞，碰撞时间很短可忽略不计，碰撞为弹性碰撞，两小球可视为质点．当乙球刚运动到D处时，两小球发生第二次碰撞．求：
（1）第一次碰撞前甲所受轨道弹力的大小；
（2）甲、乙两球质量之比
；
（3）甲与乙第二次碰撞后各自速度的大小.
如图所示，倾角为
的“U”型金属框架下端连接一阻值为
的电阻，相互平行的金属杆MN、PQ间距为
，与金属杆垂直的虚线
、
区域内有垂直框架平面向上的匀强磁场，磁感应强度大小为
，、间距离为
，一长为、质量为
、电阻为的导体棒在全属框架平面上与磁场上边界距离处从静止开始释放，最后能匀速通过磁场下边界．重力加速度为
（金属框架摩擦及电阻不计）．求：
（1）导体棒刚到达磁场上边界时速度大小
；
（2）导体棒匀速通过磁场下边界时速度大小
；
（3）导体棒穿越磁场过程中，回路产生的电能．
如图所示，空间有相互垂直的匀强电场和匀强磁场交界于虚线，电场强度为
，虚线下方匀强磁场范围足够大，磁感应强度为
，现有质量为
、电量为
的带正电粒子从距电磁场边界
处无初速释放（带电粒子重力可忽略不计）．求：
（1）带电粒子刚离开电场时速度大小；
（2）带电粒子在匀强磁场中运动的轨迹半径；
（3）带电粒子第一次在匀强磁场中运动的时间.
如图所示，A、B、C、D、E为波沿传播方向上间距均为d=1m的五个质点，一简谐横波以5m/s的水平速度向右传播，t=0时刻到达质点A且A开始向上振动，其振动周期为0.4s，试求：
①该简谐波的波长;
②自0时刻起到质点E第一次到达波谷的时间.
,在压缩前其气缸内气体温度为
，压强为
，在压缩冲程末，气缸内气体体积被压缩为
，若要求此时缸内气体温度达到
，则此时的气缸壁将承受多大的气压？（视缸内气体为理想气体）
粤公网安备 44130202000953号