(14分)质量m＝1 kg的物体，在水平拉力F(拉力方向与物体初速度方向相同)
的作用下，沿粗糙水平面运动，经过位移4 m时，拉力F停止作用，运动到位
移是8 m时物体停止，运动过程中Ek－x的图线如图10所示．求：(g取10 m/s2)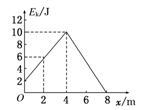
(1)物体的初速度多大？
(2)物体和平面间的动摩擦因数为多大？
(3)拉力F的大小．
如图所示，一个放置在水平地面上的木块，其质量为m=2kg，受到一个斜向下的、与水平方向成30o角的推力F=10N的作用，使木块从静止开始运动，5s后撤去推力。若木块与地面间的动摩擦因数μ=0.1，求木块在地面上运动的总位移。(g=10m/s2,
)
如图所示，质量为M=6kg的物体处于静止状态，OB细绳与水平方向夹角为37°。
求：OA、OB两根细绳的拉力大小。（sin37°=0.6,cos37°=0.8） 
一个质量m=3kg的物体放在一长木板上，当木板一端抬起使它与水平方向成θ=30°时，物体正好可以沿板面匀速下滑。当木板水平放置时，用多大的水平拉力才能将物体拉动？（设物体受到的最大静摩擦力等于滑动摩擦力）
如图所示，两根足够长的光滑金属导轨MN、PQ间距为l=0.5m，其电阻不计，两导轨及其构成的平面均与水平面成30°角。完全相同的两金属棒ab、cd分别垂直导轨放置，每棒两端都与导轨始终有良好接触，已知两棒的质量均为0.02kg，电阻均为R=0.1Ω，整个装置处在垂直于导轨平面向上的匀强磁场中，磁感应强度为B=0.2T，棒ab在平行于导轨向上的力F作用下，沿导轨向上匀速运动，而棒cd恰好能保持静止。取g="10m/s" 2，
问：（1）通过cd棒的电流I是多少，方向如何？
（2）棒ab受到的力F多大？
（3）当电流通过电路产生的焦耳热为Q=0.2J时，力F做的功W是多少？
粤公网安备 44130202000953号