如图12－1－17所示，置于空气中的一不透明容器内盛满某种透明液体．容器底部靠近器壁处有一竖直放置的6.0 cm长的线光源．靠近线光源一侧的液面上盖有一遮光板，另一侧有一水平放置的与液面等高的望远镜，用来观察线光源．开始时通过望远镜不能看到线光源的任何一部分．将线光源沿容器底向望远镜一侧平移至某处时，通过望远镜刚好可以看到线光源底端．再将线光源沿同一方向移动8.0 cm，刚好可以看到其顶端．求此液体的折射率n.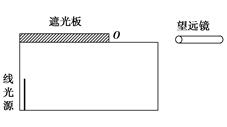
图12－1－17
如图所示，一根直棒长度为5m，用手提着其上端，在其下端的正下方10m处有一长度为5m的、内径比直棒大得多的空心竖直管子，放开后让直棒做自由落体运动（不计空气阻力，重力加速度取g=10m∕s2）。求：
（1）直棒下端下落至空心管上端时所用的时间；
（2）直棒通过该空心管所用的时间。
如图所示，在xoy直角坐标系中，第Ⅰ象限内分布着方向垂直纸面向里的匀强磁场，第二象限内分布着方向沿y轴负方向的匀强电场。初速度为零、带电量为q、质量为m的离子经过电压为U的电场加速后，从x上的A点垂直x轴进入磁场区域，经磁场偏转后过y轴上的P点且垂直y轴进入电场区域，在电场偏转并击中x轴上的C点。已知OA=OC=d。不计重力。求；
（1）粒子到达A点的速度；
（2）磁感强度B和电场强度E的大小；
如图所示，在x轴的上方（y＞0的空间内）存在着垂直于纸面向里、磁感应强度为B的匀强磁场，一个不计重力的带正电粒子从坐标原点O处以速度v进入磁场，粒子进入磁场时的速度方向垂直于磁场且与x轴正方向成45°角，若粒子的质量为m，电量为q，求：
（1）该粒子在磁场中作圆周运动的轨道半径；
（2）粒子在磁场中运动的时间；
（3）该粒子射出磁场的位置。
电磁炮是一种理想的兵器，它的主要原理如图所示。1982年澳大利亚制成了能把m= 2.0kg的弹体（包括金属杆EF的质量）加速到10km/s的电磁炮（常规炮弹的速度约为2km/s）。若轨道宽为2m，通过的电流为10A，轨道间所加匀强磁场的磁感强度为B=5×1O4T，B垂直于轨道向上 （轨道摩擦不计）求：
（1）弹体（包括金属杆EF）所受安培力大小；
（2）弹体（包括金属杆EF）从静止加速到10km/s，轨道至少要多长；
（3）弹体（包括金属杆EF）从静止加速到10km/s过程中，安培力
的最大瞬时功率。
粤公网安备 44130202000953号