如图所示，物体A的质量M=2kg和物体B的质量m=1kg，通过轻绳子跨过滑轮相连。斜面光滑，不计绳子和滑轮之间的摩擦。开始时A物体离地的高度为h=0.4m，B物体位于斜面的底端斜面倾角为θ=30°，刚开始时用手托住A物体，使A、B两物均处于静止状态。重力加速度g=10m/s²，撤去手后，求：
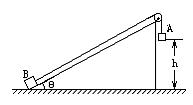
（1）A物体落地瞬间的速度大小？
（2）A物体落地后B物体还能够继续沿斜面向上滑多远？
如图所示，轨道ABCD的AB段为一半径R=0.2
的光滑1/4圆形轨道，BC段为高为h=5的竖直轨道，CD段为水平轨道。一质量为0.1
的小球由A点从静止开始下滑到B点时速度的大小为2/s，离开B点做平抛运动（g取10/s2），求：
①小球离开B点后，在CD轨道上的落地点到C的水平距离；
②小球到达B点时对圆形轨道的压力大小？
③如果在BCD轨道上放置一个倾角
＝45°的斜面（如图中虚线所示），那么小球离开B点后能否落到斜面上？如果能，求它第一次落在斜面上的位置。
如图，置于圆形水平转台边缘的小物块随转台加速转动，当转速达到某一数值时，物块恰好滑离转台开始做平抛运动。现测得转台半径R="0.5" m,离水平地面的高度H=0.8m,物块平抛落地过程水平位移的大小s=0.4m。设物块所受的最大静摩擦力等于滑动摩擦力，取重力加速度g=10m/s2。求：
（1）物块做平抛运动的初速度大小v0；
（2）物块与转台间的动摩擦因数μ。
(10分)如图所示，质量为15kg的物体用两根绳子AO和BO吊挂在天花板下处于静止状态，绳AO、BO与竖直方向的夹角分别为53°、37°。（sin37°=0.6,cos37°=0.8，取g=10m/s2）
（1）求两根绳子受到的拉力大小。(6分)
（2）如果绳AO、BO的最大承受力都是200N，为了使绳子不被拉断，则所挂的重物的质量最多不能超过多少？(4分)
某一长直的赛道上，有一辆F1赛车，前方200m处有一安全车正以
的速度匀速前进，这时赛车从静止出发以
的加速度追赶；求：
（1）赛车出发多长时间追上安全车？（ 5分）
（2）当赛车刚追上安全车时，赛车手立即刹车，使赛车以
的加速度做匀减速直线运动，再经过多长时间两车第二次相遇？
粤公网安备 44130202000953号