如图所示为玻璃制成的圆柱体,它的折射率为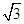 ,一细光线垂直圆柱体的轴线以i1=60°的入射角射入圆柱体。
,一细光线垂直圆柱体的轴线以i1=60°的入射角射入圆柱体。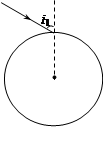
(1)求出光进入圆柱体的折射角大小
(2)作出光线穿过圆柱体并射出圆柱体的光路图。
(3)求出该光线从圆柱体中射出时,出射光线偏离原入射光线方向的角度。
如图所示为玻璃制成的圆柱体,它的折射率为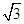 ,一细光线垂直圆柱体的轴线以i1=60°的入射角射入圆柱体。
,一细光线垂直圆柱体的轴线以i1=60°的入射角射入圆柱体。
(1)求出光进入圆柱体的折射角大小
(2)作出光线穿过圆柱体并射出圆柱体的光路图。
(3)求出该光线从圆柱体中射出时,出射光线偏离原入射光线方向的角度。