(11分)有一种叫“飞椅”的游乐项目,示意图如图9所示,长 为L的钢绳一端系着座椅,另一端固定在半径为r的水平转盘边缘,转盘可绕穿过其中心的竖直轴转动.当转盘以角速度ω匀速转动时,钢绳与转轴在同一竖直平面内,与竖直方向的夹角为θ,不计钢绳的重力,求转盘转动的角速度ω与夹角θ的关系.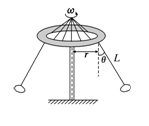
(11分)有一种叫“飞椅”的游乐项目,示意图如图9所示,长 为L的钢绳一端系着座椅,另一端固定在半径为r的水平转盘边缘,转盘可绕穿过其中心的竖直轴转动.当转盘以角速度ω匀速转动时,钢绳与转轴在同一竖直平面内,与竖直方向的夹角为θ,不计钢绳的重力,求转盘转动的角速度ω与夹角θ的关系.