电压u=120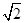 sinωt V,频率为50 Hz的交变电流,把它加在激发电压和熄灭电压均为u0=60
sinωt V,频率为50 Hz的交变电流,把它加在激发电压和熄灭电压均为u0=60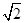 V的霓虹灯的两端.
V的霓虹灯的两端.
(1)求在一个小时内,霓虹灯发光时间有多长?
(2)试分析为什么人眼不能感到这种忽明忽暗的现象?(已知人眼的视觉暂留时间约为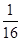 s)
s)
相关知识点
电压u=120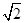 sinωt V,频率为50 Hz的交变电流,把它加在激发电压和熄灭电压均为u0=60
sinωt V,频率为50 Hz的交变电流,把它加在激发电压和熄灭电压均为u0=60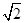 V的霓虹灯的两端.
V的霓虹灯的两端.
(1)求在一个小时内,霓虹灯发光时间有多长?
(2)试分析为什么人眼不能感到这种忽明忽暗的现象?(已知人眼的视觉暂留时间约为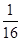 s)
s)