如图所示，在倾角θ＝37°的足够长的固定的斜面底端有一质量m＝1.0 kg的物体，物体与斜面间动摩擦因数μ＝0.25，现用轻细绳将物体由静止沿斜面向上拉动，拉力F＝10.0 N，方向平行斜面向上，经时间t1＝4.0 s绳子突然断了，(sin37°＝0.60，cos37°＝0.80，g＝10 m/s2)求：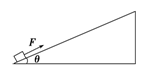
(1)绳断时物体的速度大小；
(2)从绳子断开到物体再返回到斜面底端的运动时间？
如图所示，真空中有以（r，0）为圆心，半径为 r 的圆形匀强磁场区域，磁场的磁感应强度大小为 B ，方向垂直于纸面向里，在 y =" r" 的虚线上方足够大的范围内，有水平向左的匀强电场，电场强度的大小为 E ，现在有一质子从O点沿与 x 轴正方向斜向下成 30o方向（如图中所示）射入磁场，经过一段时间后由M点（图中没有标出）穿过y轴。已知质子在磁场中做匀速圆周运动的半径也为 r ，质子的电荷量为 e ，质量为 m ，不计重力 、阻力。求：
（1）质子运动的初速度大小
（2）M点的坐标
（3）质子由O点运动到M点所用时间.
如图所示（俯视图），相距为2L的光滑平行金属导轨水平放置，导轨的一部分处在以
为右边界的匀强磁场中，匀强磁场的磁感应强大小为B，方向垂直导轨平面向下，导轨右侧接有定值电阻R，导轨电阻忽略不计。在距边界为L处垂直导轨放置一质量为m、电阻不计的金属杆ab。求解以下问题：
（1）若金属杆ab固定在导轨上的初始位置，磁场的磁感应强度在时间t内由B均匀减小到0，求此过程中电阻R上产生的焦耳热
。
（2）若磁场的磁感应强度不变，金属杆ab在恒力的作用下由静止开始向右运动3L的距离，其
图象如图乙所示。求：
①金属杆ab在刚要离开磁场时加速度的大小；
②此过程中电阻R上产生的焦耳热
。
如图所示，轨道ABC被竖直地固定在水平桌面上，A距离水平地面高H =" 0.75" m，C距离水平地面高h =" 0.45" m。一质量m = 0.10kg的小物块自A点从静止开始下滑，从C点以水平速度飞出后落在水平地面上的D点。现测得C、D两点的水平距离为x=" 0.60" m。不计空气阻力，取g =" 10" m/s2。求：
（1）小物块从C点运动到D点经历的时间；
（2）小物块从C点飞出时速度的大小；
（3）小物块从A点运动到C点的过程中克服摩擦力做的功。
如图所示,在足够长的光滑水平轨道上有三个小木块A、B、C,质量分别为mA、mB、mC，且；mA=mB =" 1.Okg" ,mc = 2.O kg,其中B与C用一个轻弹簧拴接在一起，开始时整个装置处于静止状态.A和B之间有少许塑胶炸药，A的左边有一个弹性挡板.现在引爆塑胶炸药,若炸药爆炸产生的能量中有E=9.0J转化为A和B的动能,A和B分开后,A恰好在B、C之间的弹簧第一次恢复到原长时追上B，并且与B发生碰撞后粘在一起.忽略小木块和弹性挡板碰撞过程中的能量损失.求：
(1) 塑胶炸药爆炸后瞬间A与B的速度各为多大？
(2) 在A追上B之前弹簧弹性势能的最大值；
(3) A与B相碰以后弹簧弹性势能的最大值.
和磁场的磁感应强度大小B;
粤公网安备 44130202000953号