液压千斤顶是利用密闭容器内的液体能够把液体所受到的压强行各个方向传递的原理制成的。图为一小型千斤顶的结构示意图。大活塞的直径D1=20cm,小活塞B的直径D2=5cm,手柄的长度OC=50cm,小活塞与手柄的连接点到转轴O的距离OD=10cm。现用此千斤顶使质量m=4×103kg的重物升高了h=10cm。g取10m/s2,求
(i)若此千斤顶的效率为80%,在这一过程中人做的功为多少?
(ii)若此千斤顶的效率为100%,当重物上升时,人对手柄的作用力F至少要多大?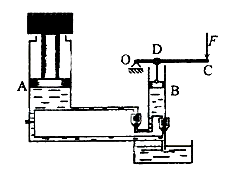
液压千斤顶是利用密闭容器内的液体能够把液体所受到的压强行各个方向传递的原理制成的。图为一小型千斤顶的结构示意图。大活塞的直径D1=20cm,小活塞B的直径D2=5cm,手柄的长度OC=50cm,小活塞与手柄的连接点到转轴O的距离OD=10cm。现用此千斤顶使质量m=4×103kg的重物升高了h=10cm。g取10m/s2,求
(i)若此千斤顶的效率为80%,在这一过程中人做的功为多少?
(ii)若此千斤顶的效率为100%,当重物上升时,人对手柄的作用力F至少要多大?