如图所示,电源电动势E=10V,内阻r=1Ω,闭合电键S后,标有“ ,
,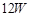 ”的灯泡恰能正常发光,电动机M绕组的电阻R0=4Ω,求:
”的灯泡恰能正常发光,电动机M绕组的电阻R0=4Ω,求:
(1)电源的输出功率P0;
(2)10s内电动机产生的热量Q;
(3)电动机的效率 ;
;
(4)若用此电动机由静止开始加速提升一质量为0.5kg的物体,10s末物体的速度达到4m/s,且在这一过程中电动机输出功率保持不变,物体也不会碰到电动机,求物体在这10s内上升的高度h(忽略空气阻力和一切摩擦作用).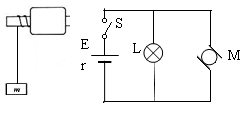
如图所示,电源电动势E=10V,内阻r=1Ω,闭合电键S后,标有“ ,
,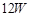 ”的灯泡恰能正常发光,电动机M绕组的电阻R0=4Ω,求:
”的灯泡恰能正常发光,电动机M绕组的电阻R0=4Ω,求:
(1)电源的输出功率P0;
(2)10s内电动机产生的热量Q;
(3)电动机的效率 ;
;
(4)若用此电动机由静止开始加速提升一质量为0.5kg的物体,10s末物体的速度达到4m/s,且在这一过程中电动机输出功率保持不变,物体也不会碰到电动机,求物体在这10s内上升的高度h(忽略空气阻力和一切摩擦作用).