一个质量m＝60 kg的滑雪运动员从高h＝20 m的高台上的A点水平滑出，落在水平地面上的B点，落地瞬间水平速度不变，竖直方向速度变为零，运动员在水平面上滑行到C点后静止，如图所示。已知A与B、B与C之间的水平距离S1＝30 m，S2＝45 m，g取10 m/s2，不计空气阻力，求：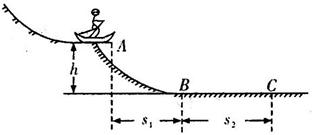
（1）运动员在A点的速度为多大？
（2）运动员在水平面BC上受到的阻力为多大？
相关试题
如图所示，导休框架中有一匀强磁场垂直穿过，磁感应强度B=0.2T，电阻R1=R2=1Ω，可动导体的电阻为0.5Ω，导体框的电阻不计，AB长度为0.5m，当AB以10m/s的速度匀速移动的过程中，求：
（1）AB两端的电压为多少？
（2）所需外力的大小为多少？
（3）外力的功率为多少瓦？
将交流电压U=
伏，接到标有“220V 100W”的灯泡两端，如果灯泡的灯丝电阻保持不变，求：
（1）通过灯泡电流的最大值是多少？
（2）灯泡的实际电功率是多少？
（3）写出电流i的瞬时值表达式，并画出i-t图象。
月球质量是地球质量的
，月球半径是地球半径的
，在距月球表面40m高处，有一质量m="60" kg的物体自由下落．
（1）它落到月球表面需要多长时间？
（2）它在月球上的重力和质量跟在地球上是否相同？（已知地球表面的重力加速度g地=9．8m/s2）
两颗靠的较近的天体称为双星，它们以两者的连线上某点为圆心做匀速圆周运动，而不会由于万有引力作用，使它们吸在一起（不考虑其他天体对它们的影响），已知两天体质量分别为m1和m2，相距为L，求它们运转的角速度
。
粤公网安备 44130202000953号