“神舟”九号飞船一飞冲天,一举成功。火箭点火竖直升空时,处于加速过程,这种状态下宇航员所受支持力F与在地表面时重力mg的比值K=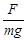 称为载荷值。(地球表面的重力加速度为g)
称为载荷值。(地球表面的重力加速度为g)
(1)假设宇航员在加速过程载荷值的最大值为K=6,求加速过程的加速度;
(2)“神舟”九号飞船发射成功后,进入轨道半径约为r=6.7×106m圆形轨道稳定运行。已知地球的半径为R=6.4×106m,估算出飞船绕地球飞行一圈需要的时间。(π2≈g)
“神舟”九号飞船一飞冲天,一举成功。火箭点火竖直升空时,处于加速过程,这种状态下宇航员所受支持力F与在地表面时重力mg的比值K=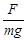 称为载荷值。(地球表面的重力加速度为g)
称为载荷值。(地球表面的重力加速度为g)
(1)假设宇航员在加速过程载荷值的最大值为K=6,求加速过程的加速度;
(2)“神舟”九号飞船发射成功后,进入轨道半径约为r=6.7×106m圆形轨道稳定运行。已知地球的半径为R=6.4×106m,估算出飞船绕地球飞行一圈需要的时间。(π2≈g)