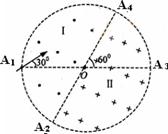
如右图所示，在一个圆形区域内，两个方向相反且都垂直于纸面的匀强磁场分布在以直径A₂A₄为边界的两个半圆形区域Ⅰ、Ⅱ中，A₂A₄与A₁A₃的夹角为60°。一质量为m，带电量为+q的粒子以某一速度从Ⅰ区的边缘点A₁处沿与A₁A₃成30°角的方向射入磁场，随后该粒子以垂直于A₂A₄的方向经过圆心O进入Ⅱ区，最后再从A₄处射出磁场。已知该粒子从射入到射出磁场所用的时间为t,求Ⅰ区和Ⅱ区中的磁感应强度的大小。（忽略粒子重力）。