如图所示，一个质量m=0.2kg的小环系于轻质弹簧的一端，且套在光滑竖直的固定大圆环上，弹簧另一端固定于圆环的最高点A，环的半径R=0.5m，弹簧原长L0=0.5m，劲度系数k=4.8N/m，若小环从图示位置B点由静止开始滑到最低的C点，在C点弹簧的弹性势能为EP=0.6J，求：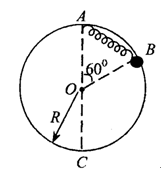
（1）小环在C处时速度
（2）小环在C点受大圆环对小环的弹力
如图所示，一轻质弹簧的一端固定在滑块B上，另一端与滑块C接触但未连接，该整体静止放在离地面高为H的光滑水平桌面上。现有一滑块A从光滑曲面上离桌面h高处由静止开始下滑下，与滑块B发生碰撞（时间极短）并粘在一起压缩弹簧推动滑块C向前运动，经一段时间，滑块C脱离弹簧，继续在水平桌面上匀速运动一段时间后从桌面边缘飞出。已知
求：
（1）滑块A与滑块B碰撞结束瞬间的速度；
（2）被压缩弹簧的最大弹性势能；
（3）滑块C落地点与桌面边缘的水平距离。
如图所示，一个
圆弧形光滑轨道ABC，放置在竖直平面内，轨道半径为R，在A 点与水平地面AD相接，地面与圆心O等高，MN是放在水平地面上长为3R、厚度不计的垫子，左端M正好位于A点。一个质量为m的小球从A处正上方某处由静止释放，不考虑空气阻力，若小球能从C点射出并打到垫子上，小球距离A点的高度在什么范围。
在水平地面上有一质量为2kg的物体，物体在水平拉力F的作用下由静止开始运动，10s后拉力大小减为F／3，该物体的运动速度随时间t的变化规律如图所示．求：
（1）物体受到的拉力F的大小．
（2）物体与地面之间的动摩擦因素．(g取10m／s2)
如图所示，轻杆BC的C点用光滑铰链与墙壁固定，杆的B点通过水平细绳AB使杆与竖直墙壁保持30°的夹角．若在B点悬挂一个定滑轮(不计重力)，某人用它匀速地提起重物．已知重物的质量 m＝30 kg，人的质量M＝50kg，g取10 m/s2.试求：
(1)此时地面对人的支持力的大小；
(2)轻杆BC和绳AB所受力的大小．
粤公网安备 44130202000953号