如图所示,质量m=1kg的小球用细线拴住,线长l=0.5m,细线所受的拉力达到F=18N时就会被拉断;当小球从图示位置释放后摆到悬点的正下方时,细线恰好被拉断;若此时小球距水平面的高度h=5m,重力加速度g取10m/s2,求小球落地处与细线恰被拉断时的位置间的距离?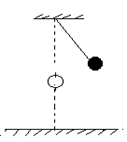
如图所示,质量m=1kg的小球用细线拴住,线长l=0.5m,细线所受的拉力达到F=18N时就会被拉断;当小球从图示位置释放后摆到悬点的正下方时,细线恰好被拉断;若此时小球距水平面的高度h=5m,重力加速度g取10m/s2,求小球落地处与细线恰被拉断时的位置间的距离?