质量 的列车,在恒定的额定功率下,沿平直的轨道由静止开始出发,在运动的过程中受到的阻力大小
的列车,在恒定的额定功率下,沿平直的轨道由静止开始出发,在运动的过程中受到的阻力大小 恒定。列车达到最大行驶速度
恒定。列车达到最大行驶速度 后,某时刻司机发现前方
后,某时刻司机发现前方 处的轨道旁山体塌方,便立即紧急刹车,这时由于刹车所附加的制动力恒为
处的轨道旁山体塌方,便立即紧急刹车,这时由于刹车所附加的制动力恒为 ,结果列车正好到达轨道毁坏处停下。求:
,结果列车正好到达轨道毁坏处停下。求:
(1)列车刹车时加速度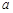 的大小;
的大小;
(2)列车在正常行驶过程中所受的阻力 的大小;(5分)
的大小;(5分)
(3)列车的额定功率 。
。
质量 的列车,在恒定的额定功率下,沿平直的轨道由静止开始出发,在运动的过程中受到的阻力大小
的列车,在恒定的额定功率下,沿平直的轨道由静止开始出发,在运动的过程中受到的阻力大小 恒定。列车达到最大行驶速度
恒定。列车达到最大行驶速度 后,某时刻司机发现前方
后,某时刻司机发现前方 处的轨道旁山体塌方,便立即紧急刹车,这时由于刹车所附加的制动力恒为
处的轨道旁山体塌方,便立即紧急刹车,这时由于刹车所附加的制动力恒为 ,结果列车正好到达轨道毁坏处停下。求:
,结果列车正好到达轨道毁坏处停下。求:
(1)列车刹车时加速度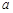 的大小;
的大小;
(2)列车在正常行驶过程中所受的阻力 的大小;(5分)
的大小;(5分)
(3)列车的额定功率 。
。