如图所示,一个质量为m的小孩在平台上以加速度a做匀加速助跑,目的是抓住在平台右端的、上端固定的、长度为L的轻质悬绳,并在竖直面内做圆周运动.已知轻质绳的下端与小孩的重心在同一高度,小孩抓住绳的瞬间重心的高度不变,且无能量损失.若小孩能完成圆周运动,则: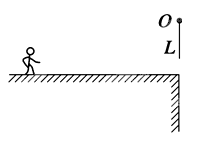
(1) 小孩抓住绳的瞬间对悬线的拉力至少为多大?
(2) 小孩的最小助跑位移多大?
（3）设小孩在加速过程中，脚与地面不打滑，求地面对脚的摩擦力大小以及摩擦力对小孩所做的功。
倍。求塔高。（不计空气阻力；取
）两块平行金属板MN、PQ水平放置，两板间距为d、板长为
，在平行板右侧的正三角形区域内存在着垂直纸面的匀强磁场，三角形底边BC与PQ在同一水平线上，顶点A与MN在同一水平线上，如图所示．一个质量为m、电量为+q的粒子沿两板中心线以初速度v0水平射入，若在两板间加某一恒定电压，粒子离开电场后垂直AB边从D点进入磁场，BD=
AB，并垂直AC边射出(不计粒子的重力)．求：
(1)两极板间电压；
(2)三角形区域内磁感应强度；
(3)若两板间不加电压，三角形区域内的磁场方向垂直纸面向外．要使粒子进入磁场区域后能从AB边射出，试求所加磁场的磁感应强度最小值．
如图所示，粗糙的斜面
下端与光滑的圆弧轨道
相切于
，整个装置竖直放置，
是最低点，圆心角
，
与圆心
等高．圆弧轨道半径
0．5 m，斜面长
。现有一个质量
0．1 kg的小物体
从斜面上端
点无初速下滑，物体与斜面之间的动摩擦因数为
(已知
,g=10m/s2)。求：
（1）物体第一次通过点时的速度大小和对点处轨道的压力各为多大?
（2）物体第一次离开点后在空中做竖直上抛运动，不计空气阻力，则最高点
和点之间的高度差为多大?
（3）物体从空中又返回到圆轨道和斜面．多次反复，在整个运动过程中，物体对点处轨道的最小压力为多大?
如图所示，宇航员站在某质量分布均匀的星球表面一斜坡上P点，沿水平方向以初速度v0抛出一个小球，测得小球经时间t落到斜坡上另一点Q，斜面的倾角为α，已知该星球的半径为R，万有引力常量为G。求该星球的密度。
如图（a）所示，A、B为两块平行金属板，极板间电压为
，板中央有小孔O和O＇。现有足够多的电子源源不断地从小孔O由静止进入A、B之间。在B板右侧，平行金属板M、N长L1=4×10-2m，板间距离d=4×10-3m，在距离M、N右侧边缘L2=0.1m处有一荧光屏P，当M、N之间未加电压时电子沿M板的下边沿穿过，打在荧光屏上的
并发出荧光。现给金属板M、N之间加一个如图（b）所示的变化电压u1，在t=0时刻，M板电势低于N板。已知电子质量为
kg，电量为
C。（1）每个电子从B板上的小孔O＇射出时的速度多大？（2）打在荧光屏上的电子范围是多少?（3）打在荧光屏上的电子的最大动能是多少？
粤公网安备 44130202000953号