在竖直平面内有一个粗糙的 圆弧轨道,其半径R=0.4m,轨道的最低点距地面高度h=0.45m.一质量m=0.1kg的小滑块从轨道的最高点A由静止释放,到达最低点B时以一定的水平速度离开轨道,落地点C距轨道最低点的水平距离x=0.6m.空气阻力不计,g取10m/s2,求:
圆弧轨道,其半径R=0.4m,轨道的最低点距地面高度h=0.45m.一质量m=0.1kg的小滑块从轨道的最高点A由静止释放,到达最低点B时以一定的水平速度离开轨道,落地点C距轨道最低点的水平距离x=0.6m.空气阻力不计,g取10m/s2,求: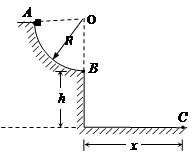
(1)小滑块离开轨道时的速度大小;
(2)小滑块运动到轨道最低点时,对轨道的压力大小;
(3)小滑块在轨道上运动的过程中,克服摩擦力所做的功.
在竖直平面内有一个粗糙的 圆弧轨道,其半径R=0.4m,轨道的最低点距地面高度h=0.45m.一质量m=0.1kg的小滑块从轨道的最高点A由静止释放,到达最低点B时以一定的水平速度离开轨道,落地点C距轨道最低点的水平距离x=0.6m.空气阻力不计,g取10m/s2,求:
圆弧轨道,其半径R=0.4m,轨道的最低点距地面高度h=0.45m.一质量m=0.1kg的小滑块从轨道的最高点A由静止释放,到达最低点B时以一定的水平速度离开轨道,落地点C距轨道最低点的水平距离x=0.6m.空气阻力不计,g取10m/s2,求:
(1)小滑块离开轨道时的速度大小;
(2)小滑块运动到轨道最低点时,对轨道的压力大小;
(3)小滑块在轨道上运动的过程中,克服摩擦力所做的功.