如图所示,Q为一个原来静止在光滑水平面上的物体,质量为M,它带有一个凹形的不光滑轨道,轨道的ab段是水平的,bc段是半径为R的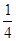 圆弧,位于竖直平面内。P是另一个小物体,质量为m,它与轨道间的动摩擦因数为μ。物体P以沿水平方向的初速度v0冲上Q的轨道,已知它恰好能到达轨道顶端c点,后又沿轨道滑下,并最终在a点停止滑动,然后与Q一起在水平面上运动。
圆弧,位于竖直平面内。P是另一个小物体,质量为m,它与轨道间的动摩擦因数为μ。物体P以沿水平方向的初速度v0冲上Q的轨道,已知它恰好能到达轨道顶端c点,后又沿轨道滑下,并最终在a点停止滑动,然后与Q一起在水平面上运动。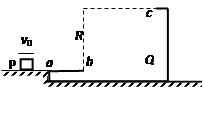
(1)分别求出P从a点滑到c点和从c点滑回a点的过程中各有多少机械能转化为内能?
(2)P位于轨道的哪个位置时,Q的速度达到最大?
如图所示,Q为一个原来静止在光滑水平面上的物体,质量为M,它带有一个凹形的不光滑轨道,轨道的ab段是水平的,bc段是半径为R的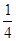 圆弧,位于竖直平面内。P是另一个小物体,质量为m,它与轨道间的动摩擦因数为μ。物体P以沿水平方向的初速度v0冲上Q的轨道,已知它恰好能到达轨道顶端c点,后又沿轨道滑下,并最终在a点停止滑动,然后与Q一起在水平面上运动。
圆弧,位于竖直平面内。P是另一个小物体,质量为m,它与轨道间的动摩擦因数为μ。物体P以沿水平方向的初速度v0冲上Q的轨道,已知它恰好能到达轨道顶端c点,后又沿轨道滑下,并最终在a点停止滑动,然后与Q一起在水平面上运动。
(1)分别求出P从a点滑到c点和从c点滑回a点的过程中各有多少机械能转化为内能?
(2)P位于轨道的哪个位置时,Q的速度达到最大?