在如图所示的空间里,存在垂直纸面向里的匀强磁场,磁感应强度为 .在竖直方向存在交替变化的匀强电场如图(竖直向上为正),电场大小为
.在竖直方向存在交替变化的匀强电场如图(竖直向上为正),电场大小为 .一倾角为θ足够长的光滑绝缘斜面放置在此空间.斜面上有一质量为m,带电量为-q的小球,从t=0时刻由静止开始沿斜面下滑,设第5秒内小球不会离开斜面,重力加速度为g
.一倾角为θ足够长的光滑绝缘斜面放置在此空间.斜面上有一质量为m,带电量为-q的小球,从t=0时刻由静止开始沿斜面下滑,设第5秒内小球不会离开斜面,重力加速度为g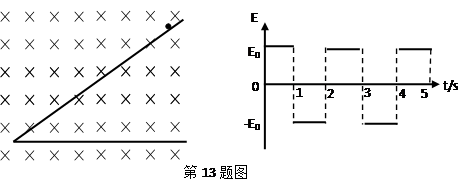
求:(1)求第1秒末小球的速度大小.
(2)第6秒内小球离开斜面的最大距离.
(3)若第19秒内小球仍未离开斜面,θ角应满足什么条件?
在如图所示的空间里,存在垂直纸面向里的匀强磁场,磁感应强度为 .在竖直方向存在交替变化的匀强电场如图(竖直向上为正),电场大小为
.在竖直方向存在交替变化的匀强电场如图(竖直向上为正),电场大小为 .一倾角为θ足够长的光滑绝缘斜面放置在此空间.斜面上有一质量为m,带电量为-q的小球,从t=0时刻由静止开始沿斜面下滑,设第5秒内小球不会离开斜面,重力加速度为g
.一倾角为θ足够长的光滑绝缘斜面放置在此空间.斜面上有一质量为m,带电量为-q的小球,从t=0时刻由静止开始沿斜面下滑,设第5秒内小球不会离开斜面,重力加速度为g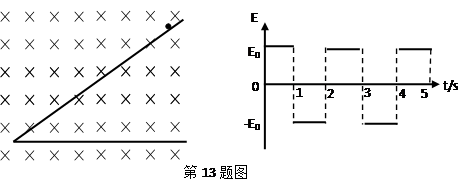
求:(1)求第1秒末小球的速度大小.
(2)第6秒内小球离开斜面的最大距离.
(3)若第19秒内小球仍未离开斜面,θ角应满足什么条件?