一赛艇停在平静的水面上,赛艇前端有一标记P离水面的高度为h1=0.6m,尾部下端Q略高于水面;赛艇正前方离赛艇前端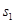 =0.8m处有一浮标,示意如图。一潜水员在浮标前方
=0.8m处有一浮标,示意如图。一潜水员在浮标前方 =3.0m处下潜到深度为
=3.0m处下潜到深度为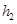 =4.0m时,看到标记刚好被浮标挡住,此处看不到船尾端Q;继续下潜△h=4.0m,恰好能看见Q。求
=4.0m时,看到标记刚好被浮标挡住,此处看不到船尾端Q;继续下潜△h=4.0m,恰好能看见Q。求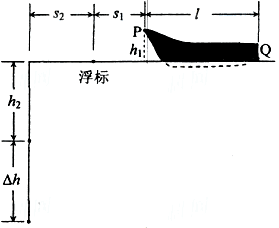
(1)水的折射率n;
(2)赛艇的长度l。(可用根式表示)
一赛艇停在平静的水面上,赛艇前端有一标记P离水面的高度为h1=0.6m,尾部下端Q略高于水面;赛艇正前方离赛艇前端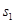 =0.8m处有一浮标,示意如图。一潜水员在浮标前方
=0.8m处有一浮标,示意如图。一潜水员在浮标前方 =3.0m处下潜到深度为
=3.0m处下潜到深度为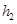 =4.0m时,看到标记刚好被浮标挡住,此处看不到船尾端Q;继续下潜△h=4.0m,恰好能看见Q。求
=4.0m时,看到标记刚好被浮标挡住,此处看不到船尾端Q;继续下潜△h=4.0m,恰好能看见Q。求
(1)水的折射率n;
(2)赛艇的长度l。(可用根式表示)