如图所示,质量均为m、可视为质点的A、B两物体紧挨着放在水平面上的O点,左边有竖直墙壁M,右边在P点与光滑的、半径为R的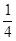 圆弧槽相连,MO=ON=R。A物体与水平面间的摩擦力忽略不计,B物体与水平面间的动摩擦因数为0.5。开始时两物体静止。现让A物体以初速度
圆弧槽相连,MO=ON=R。A物体与水平面间的摩擦力忽略不计,B物体与水平面间的动摩擦因数为0.5。开始时两物体静止。现让A物体以初速度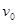 向左开始运动,设A与竖直墙壁、A与B均发生无机械能损失的碰撞。已知重力加速度为g。要使B物体第一次被A碰撞后,恰能上升至圆弧槽最高点P点,求:
向左开始运动,设A与竖直墙壁、A与B均发生无机械能损失的碰撞。已知重力加速度为g。要使B物体第一次被A碰撞后,恰能上升至圆弧槽最高点P点,求:
(a)A物体的初速度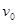 为多少?
为多少?
(b)B物体最终停在何处?
如图所示,质量均为m、可视为质点的A、B两物体紧挨着放在水平面上的O点,左边有竖直墙壁M,右边在P点与光滑的、半径为R的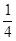 圆弧槽相连,MO=ON=R。A物体与水平面间的摩擦力忽略不计,B物体与水平面间的动摩擦因数为0.5。开始时两物体静止。现让A物体以初速度
圆弧槽相连,MO=ON=R。A物体与水平面间的摩擦力忽略不计,B物体与水平面间的动摩擦因数为0.5。开始时两物体静止。现让A物体以初速度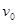 向左开始运动,设A与竖直墙壁、A与B均发生无机械能损失的碰撞。已知重力加速度为g。要使B物体第一次被A碰撞后,恰能上升至圆弧槽最高点P点,求:
向左开始运动,设A与竖直墙壁、A与B均发生无机械能损失的碰撞。已知重力加速度为g。要使B物体第一次被A碰撞后,恰能上升至圆弧槽最高点P点,求:
(a)A物体的初速度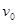 为多少?
为多少?
(b)B物体最终停在何处?