在平直铁轨上以60m/s速度行驶的动车组车箱内，乘客突然发现，悬挂在箱顶上的物体悬线向车前进方向偏离竖直方向θ＝14°角，如下图所示，从此刻起动车组保持该情形不变，求：（tan14°＝0.25，g＝10m/s2）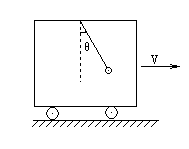
（1）动车组是匀加速直线运动还是匀减速直线运动；
（2）动车组的加速度大小；
（3）动车组若作匀减速直线运动，30s内运动的距离。
如图甲所示，两平行极板P、Q的极板长度和板间距均为l，位于极板左侧的粒子源沿极板中央向右连接发射质量为m、电量为+q、速度相同、重力不计的带电粒子,在0~3t0时间内两板间加上如图乙所示的电压（不考虑极边缘的影响）.已知t=0时刻进入两板间的带电粒子恰好在t0时刻经极板边缘射出.上述m、q、l、t0为已知量.（不考虑粒子间相互影响及返回板间的情况）
（1）求电压U0的大小.
（2）求
时进入两板间的带电粒子在离开电场时的速度大小.
(10分)把电量为
的正点电荷从无限远处移到电场中A点，电场力做功
，若把该电荷从无限远处移到电场中B点，电场力做功
，取无限远处电势为零。求：
（1）电势差UAB
（2）若把
的负电荷由A点移到B点，求电场力所做的功
（3）如图，若A、B处于竖直向上的匀强电场，A、B之间距离L=1m。A、B连线与水平方向之间夹角为370，求场强大小
(10分) 小型直流电动机（其线圈内阻为r=1
）与规格为“4V、4W”的小灯泡并联，再与阻值为R=5的电阻串联,然后接至U=12V的电压上，如图小灯泡恰好正常发光，电动机正常工作,求：
（1）通过电动机的电流 （2）电动机的输出功率P出。
一小球以20m/s的速度沿光滑斜面向上做匀减速直线运动，加速度大小为a=5m/s2，如果斜面足够长(小球沿斜面返回时加速度不变)，求：
（1）经过t=6s的时间，小球速度的大小和方向怎样.
（2）当速度大小变为10m/s时物体所通过的位移是多少?
（3）当速度大小变为10m/s时物体所通过的路程是多少?
粤公网安备 44130202000953号