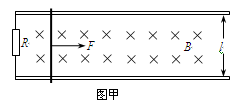
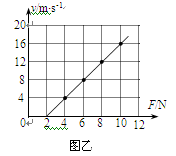
如图甲所示,固定于水平面上的两根互相平行且足够长的金属导轨,处在方向竖直向下的匀强磁场中。两导轨间距离l= 0.5m,两轨道的左端之间接有一个R=0.5W的电阻。导轨上垂直放置一根质量m=0.5kg的金属杆。金属杆与导轨的电阻忽略不计。将与导轨平行的恒定拉力F作用在金属杆上,使杆从静止开始运动,杆最终将做匀速运动。当改变拉力的大小时,相对应的匀速运动速度v也会变化,v与F的关系如图乙所示。取重力加速度g=10m/s2,金属杆与导轨间的最大静摩擦力与滑动摩擦力相等,金属杆始终与轨道垂直且它们之间保持良好接触。
(1)金属杆在匀速运动之前做什么运动?
(2)求磁感应强度B的大小,以及金属杆与导轨间的动摩擦因数μ 。