如图为一网球场长度示意图,球网高为h=0.9m,发球线离网的距离为x=6.4m,某一运动员在一次击球时,击球点刚好在发球线上方H=1.25m高处,设击球后瞬间球的速度大小为v0=32m/s,方向水平且垂直于网,试通过计算说明网球能否过网?若过网,试求网球的直接落地点离对方发球线的距离L?(不计空气阻力,重力加速度g取10m/s2)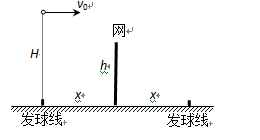
如图为一网球场长度示意图,球网高为h=0.9m,发球线离网的距离为x=6.4m,某一运动员在一次击球时,击球点刚好在发球线上方H=1.25m高处,设击球后瞬间球的速度大小为v0=32m/s,方向水平且垂直于网,试通过计算说明网球能否过网?若过网,试求网球的直接落地点离对方发球线的距离L?(不计空气阻力,重力加速度g取10m/s2)