如图所示,水平U形光滑框架,宽度为1m,电阻忽略不计,导体ab质量是0.2kg,电阻是0.1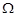 ,匀强磁场的磁感应强度B=0.1T,方向垂直框架向上,现用1N的外力F由静止拉动ab杆,当ab的速度达到1m/s时,
,匀强磁场的磁感应强度B=0.1T,方向垂直框架向上,现用1N的外力F由静止拉动ab杆,当ab的速度达到1m/s时,
(1)求此时刻ab杆产生的感应电动势的大小;
(2)求此时刻ab杆的加速度的大小?
(3)ab杆所能达到的最大速度是多少?
如图所示,水平U形光滑框架,宽度为1m,电阻忽略不计,导体ab质量是0.2kg,电阻是0.1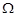 ,匀强磁场的磁感应强度B=0.1T,方向垂直框架向上,现用1N的外力F由静止拉动ab杆,当ab的速度达到1m/s时,
,匀强磁场的磁感应强度B=0.1T,方向垂直框架向上,现用1N的外力F由静止拉动ab杆,当ab的速度达到1m/s时,
(1)求此时刻ab杆产生的感应电动势的大小;
(2)求此时刻ab杆的加速度的大小?
(3)ab杆所能达到的最大速度是多少?