一根长为l的绝缘细线一端固定,另一端连着一质量为m的带正电A球,置于水平向左的电场中,已知A球所受的电场力大小为 。另有一质量为2m的B球静止地悬挂在一弹簧下端(B球与弹簧均为绝缘材料制成),弹簧伸长
。另有一质量为2m的B球静止地悬挂在一弹簧下端(B球与弹簧均为绝缘材料制成),弹簧伸长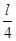 ,现让A球沿如图虚线上摆,摆到水平位置时速度
,现让A球沿如图虚线上摆,摆到水平位置时速度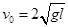 ,恰好与B球发生正碰,B球受碰后向上振动,到达最高点时,弹簧被压缩
,恰好与B球发生正碰,B球受碰后向上振动,到达最高点时,弹簧被压缩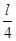 。求:A球回到最低点M时细线受到的拉力大小。
。求:A球回到最低点M时细线受到的拉力大小。 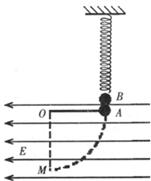
一根长为l的绝缘细线一端固定,另一端连着一质量为m的带正电A球,置于水平向左的电场中,已知A球所受的电场力大小为 。另有一质量为2m的B球静止地悬挂在一弹簧下端(B球与弹簧均为绝缘材料制成),弹簧伸长
。另有一质量为2m的B球静止地悬挂在一弹簧下端(B球与弹簧均为绝缘材料制成),弹簧伸长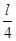 ,现让A球沿如图虚线上摆,摆到水平位置时速度
,现让A球沿如图虚线上摆,摆到水平位置时速度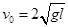 ,恰好与B球发生正碰,B球受碰后向上振动,到达最高点时,弹簧被压缩
,恰好与B球发生正碰,B球受碰后向上振动,到达最高点时,弹簧被压缩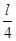 。求:A球回到最低点M时细线受到的拉力大小。
。求:A球回到最低点M时细线受到的拉力大小。 