如图所示,足够长的光滑金属框竖直放置,框宽L=0.5 m框的电阻不计,匀强磁场磁感应强度B=1 T,方向与框面垂直,金属棒MN的质量为100 g,电阻为1 Ω.现让MN无初速地释放并与框保持接触良好的竖直下落,从释放到达到最大速度的过程中通过棒某一横截面的电量为2 C,求此过程中回路产生的电能.(空气阻力不计,g=10 m/s2)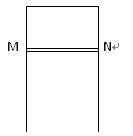
如图所示,足够长的光滑金属框竖直放置,框宽L=0.5 m框的电阻不计,匀强磁场磁感应强度B=1 T,方向与框面垂直,金属棒MN的质量为100 g,电阻为1 Ω.现让MN无初速地释放并与框保持接触良好的竖直下落,从释放到达到最大速度的过程中通过棒某一横截面的电量为2 C,求此过程中回路产生的电能.(空气阻力不计,g=10 m/s2)