如图所示,半径为R的光滑半圆环轨道竖直固定在一水平光滑的桌面上,在桌面上轻
质弹簧被a、b两个小球挤压(小球与弹簧不拴接),处于静止状态。同时释放两个小球,
小球a、b与弹簧在桌面上分离后,a球从B点滑上光滑半圆环轨道最高点A时速度为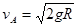 。已知小球a质量为m,小球b质量为2m,重力加速度为g。求:
。已知小球a质量为m,小球b质量为2m,重力加速度为g。求:
(1)小球a在圆环轨道最高点对轨道的压力;
(2)释放后小球b离开弹簧时的速度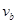 的大小;
的大小;
(3)释放小球前弹簧具有的弹性势能。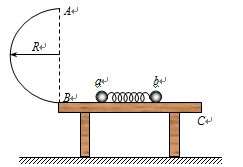
如图所示,半径为R的光滑半圆环轨道竖直固定在一水平光滑的桌面上,在桌面上轻
质弹簧被a、b两个小球挤压(小球与弹簧不拴接),处于静止状态。同时释放两个小球,
小球a、b与弹簧在桌面上分离后,a球从B点滑上光滑半圆环轨道最高点A时速度为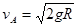 。已知小球a质量为m,小球b质量为2m,重力加速度为g。求:
。已知小球a质量为m,小球b质量为2m,重力加速度为g。求:
(1)小球a在圆环轨道最高点对轨道的压力;
(2)释放后小球b离开弹簧时的速度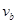 的大小;
的大小;
(3)释放小球前弹簧具有的弹性势能。