如图所示,细绳一端系着质量m="0.1" kg的小物块A,置于光滑水平台面上;另一端通过光滑小孔O与质量M="0.5" kg的物体B相连,B静止于水平地面上。当A以O为圆心做半径r =0.2m的匀速圆周运动时,地面对B的支持力F =3.0N,求物块A的速度ν和角速度ω的大小。(g=10m/s2)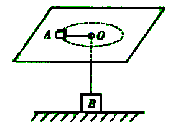
如图所示,细绳一端系着质量m="0.1" kg的小物块A,置于光滑水平台面上;另一端通过光滑小孔O与质量M="0.5" kg的物体B相连,B静止于水平地面上。当A以O为圆心做半径r =0.2m的匀速圆周运动时,地面对B的支持力F =3.0N,求物块A的速度ν和角速度ω的大小。(g=10m/s2)